Friday, August 3, 2018

DEFLECTION OF BEAM

DEFLECTION OF BEAM USING MACALYS METHOD

Determine the

1) The elastic curve for both slope and deflection2) Deflection at mid-span3) Position where deflection is maximum4) slope and deflection at x=1; 1.5; and x=3 of the loaded beam shown below





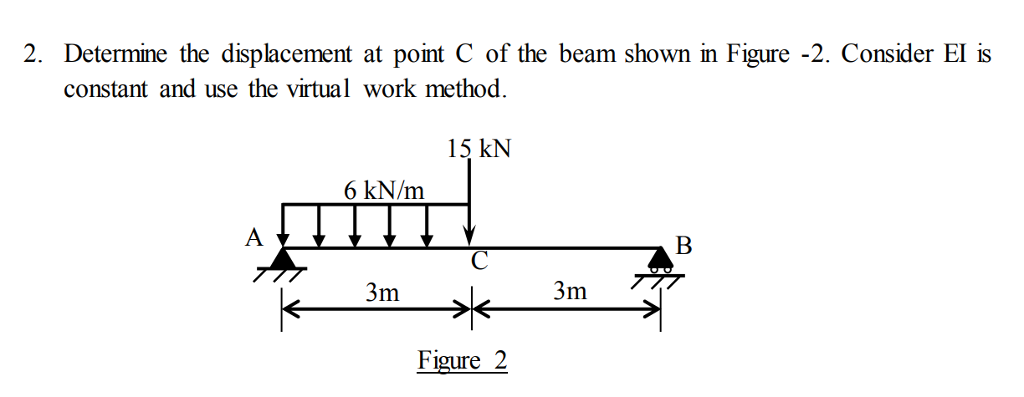
DEFLECTION OF BEAM USING VIRTUAL WORK METHOD

2. Determine the displacement at point C of the beam shown in Figure -2. Consider El is constant and use the virtual work method 15 kN 6 kN/m 3m Figure 2



DEFLECTION OF BEAM USING CONJUGATE BEAM METHOD

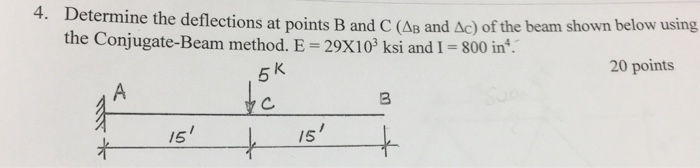
4. Determine the deflections at poi the Conjugate-Beam method. E- 29X103 ksi and I -800 in. nts B and C AB and ?c) of the beam shown below using 20 points 5 3 15 15



DEFLECTION OF BEAM USING SUPERPOSITION METHOD

Part C-Advanced Question This question is designed for students who seek to obtain a mark of Distinction or higher. It is not necessarily mathematically difficult, but requires more thinking, visualisation, and application than the other questions. The majority of marks will be awarded for completed questions, and only minor marks will be awarded for partially answered questions. The marks awarded in this section are bonus marks. 5) 10 Marks Consider a cantilever of total length L. The beam experiences 3 vertical point loads, each of magnitude P, acting at L/3, 2L/3 and L along the beam. The beam has a constant cross-section with second moment of area /and demonstrates linear elastic behaviour with elastic modulus E. What is the maximum deflection of the beam in terms of P, I, E and L? (Sufficient working to justify your answer is required) You may take advantage of the standard case of a cantilever with a single point load at the tip. In class it was shown that the deflected shape takes the form


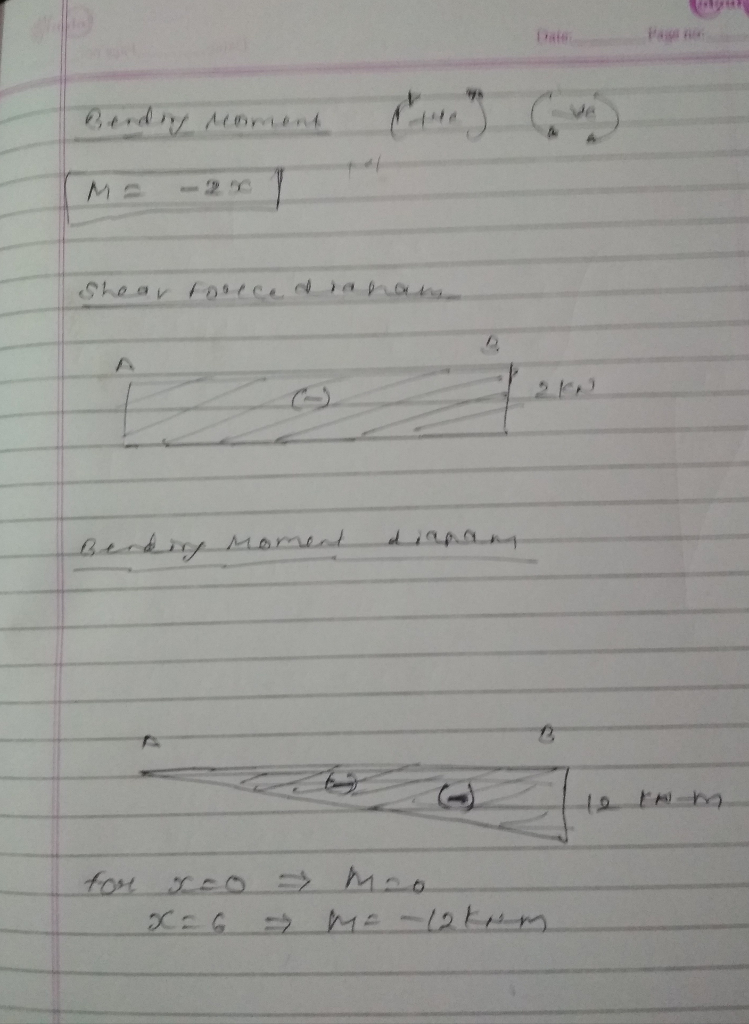
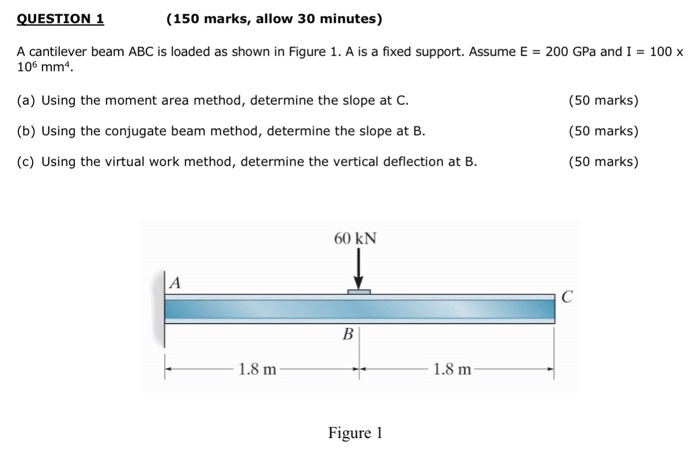
CALCULATE THE SLOPE AND DEFLECTION USING MOMENT AREA, CONJUGATE BEAM AND VIRTUAL LOAD OF CANTILEVERED BEAM

QUESTION 1 (150 marks, allow 30 minutes) A cantilever beam ABC is loaded as shown in Figure 1, A is a fixed support. Assume E = 200 GPa and I = 100 x 106 mm4. (a) Using the moment area method, determine the slope at C (b) Using the conjugate beam method, determine the slope at B (c) Using the virtual work method, determine the vertical deflection at B. (50 marks) (50 marks) (50 marks) 60 kN 1.8 m 1.8 m Figure 1



CALCULATE THE DEFLECTION AT MIDPOINT OF BEAM AND EQUATION OF ELASTIC CURVE



 MAXIMUM DEFLECTION OF BEAM USING DOUBLE INTEGRATION METHOD













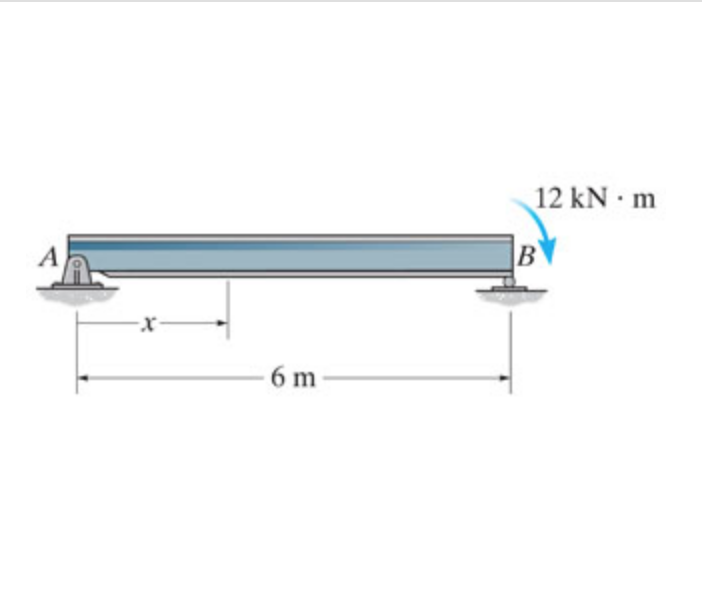
12 kN m





Posted by at

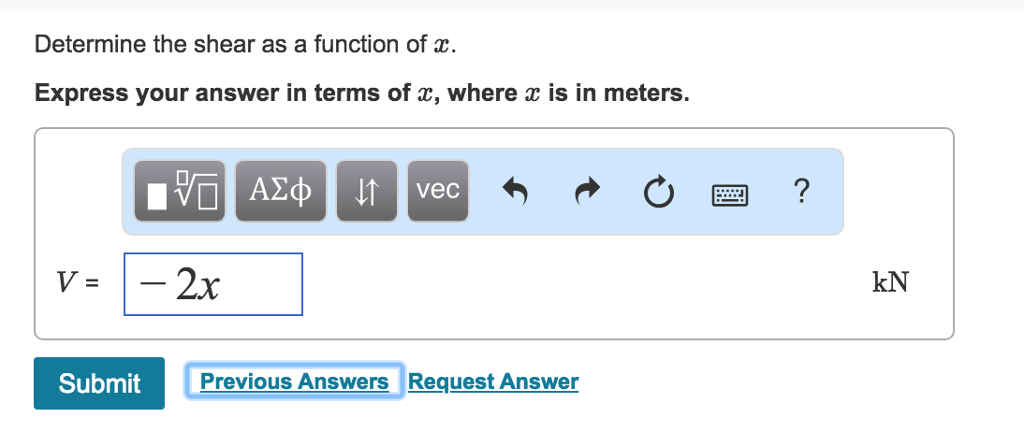
No comments:

Post a Comment

Subscribe to: Post Comments (Atom)